funcionando-ya

Las simetrías son muy fáciles de observar en las gráficas de las funciones. Primero, tengamos claro que existen varios tipos de simetría. Vamos a ver las más importantes. Por ejemplo, un objeto puede ser simétrico a otro respecto de un determinado eje, como ocurre con el dibujo del pez del ejemplo:

Estos objetos son simétricos respecto del eje a. En funciones, tenemos que una función puede ser simétrica respecto del eje y, como la del ejemplo:

Gráficamente es muy fácil de observar la simetría. Matemáticamente lo que tenemos es que f(x)=f(-x). Es decir, que a la abscisa x=2 le va a corresponder la misma ordenada o y que a la abscisa x=-2. Pincha aquí para verlo más claramente.

Podemos encontrar también la denominada simetría respecto al origen. En este caso tenemos que f(x)=-f(-x). Gráficamente se observa que es como si la función se reflejara en la recta que divide en dos partes iguales a los cuadrantes 2º y 4º, es decir, dicha recta es ahora el eje de simetría:

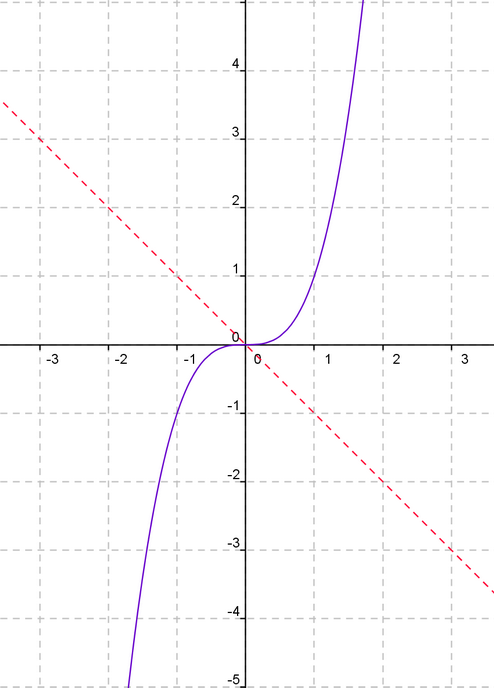
Matemáticamente lo que tenemos es que si para x=1 la ordenada es y=1, tendremos que para la abscisa opuesta (x=-1), la ordenada es la opuesta también (y=-1). Pincha aquí para verlo mejor.