Gráfica
Una función la podemos expresar de las siguientes formas:
1) Con su expresión verbal: “La variable y se obtiene al sumar uno al doble de la variable x”.
2) Con su expresión algebraica: y = 2x + 1. Observa que la expresión algebraica la obtienes al traducir la expresión verbal a lenguaje algebraico y viceversa.
3) Con su gráfica… pero ¿qué es la gráfica de la función y cómo se obtiene?
La gráfica de la función es algo así como “la foto” de la función. Dado que una función es una relación (entre la variable x y la variable y), he de obtener un dibujo que represente esa relación. Para ello tengo que dibujar qué único valor de la variable y le corresponde a cada valor de la variable x del dominio de la función. Utilizaremos un sistema de referencia cartesiano. Para referenciar la posición de cualquier objeto en el plano necesitamos un punto respecto al cual referenciar dicha posición. Ese punto será el origen, O, de nuestro sistema de referencia y es el punto en el cual se cortan los ejes de coordenadas cartesianas, los cuales son dos rectas perpendiculares entre sí:

Observa que hemos dividido los ejes en unidades iguales y adoptamos el siguiente convenio:

Así, para dar la posición de un punto daremos su par de coordenadas de la forma (coordenada x, coordenada y) indicando entonces primero su distancia en horizontal respecto de O (pudiendo ser positiva o negativa dependiendo del cuadrante en el que esté situado) y luego su distancia en vertical respecto de O que análogamente será positiva o negativa.
Observando el gráfico vemos que:
| Primer cuadrante | Segundo cuadrante | Tercer cuadrante | Cuarto cuadrante | |
|---|---|---|---|---|
| abscisa |
+
|
-
|
-
|
+
|
| ordenada |
+
|
+
|
-
|
-
|
| ejemplo |
(3, 5)
|
(-3, 5)
|
(-3, -5)
|
(3, -5)
|

Decimos que queremos obtener algo así como “la foto” de la función…

…sí, ¡pero no precisamente esta!
Dado que la gráfica de la función pretende representar qué único valor de la variable y le corresponde a cada uno de los valores de la variable x del dominio de la función, si esos pares de valores relacionados (x,y) los consideramos las coordenadas de puntos y representamos dichos puntos en los ejes de coordenadas, lograríamos nuestro objetivo de obtener una “foto” de la función, de ver dibujada la relación que expresa.
Pero…¿cómo conseguimos esos pares de valores relacionados? Para eso tenemos la expresión algebraica. Retomemos el ejemplo y=2x + 1. Si estudiamos su dominio nos damos cuenta de que podemos introducir cualquier valor de x y la función no se “estropea”, así que el dominio son todos los reales. Elijamos diferentes valores de x y calculemos su y:
| Entrada | Salida | Punto(x,y) |
|---|---|---|
|
x = 1
|
y = 2·1+1=3
|
(1,3)
|
|
x = -1
|
y = 2·(-1)+1=-1
|
(-1,-1)
|
|
x = 0
|
y = 2·0+1=1
|
(0,1)
|
|
x = 3
|
y = 2·3+1=7
|
(3,7)
|
Dibujemos estos puntos para ver si tenemos al menos una idea de la gráfica de la función:

En ocasiones, como en este caso, no harían falta más puntos porque vemos claramente que los puntos se alinean formando una recta, pero…¿podemos unir alegremente esos puntos y obtener entonces la gráfica de la función? Eso depende de cuál es el dominio de la función. En nuestro caso el dominio de la función son todos los números reales, así que tiene sentido unir los puntos mediante la recta que “esbozan” los cuatro puntos hallados, ya que así representaremos los infinitos puntos relacionados por nuestra función que estarán a lo largo de esa recta. Así la foto definitiva de nuestra función “cazada” sería esta:


No siempre se pueden unir los puntos. Imagínate el siguiente caso en el que la función y = 2x + 1 nos da el número de botes de refresco necesarios (y) dependiendo del número de invitados a la fiesta (x). No tiene sentido unir los puntos, ya que no vamos a tener un invitado y medio (x = 1.5), el dominio de la función son sólo los números naturales y por tanto la gráfica de la función estaría constituida por puntos no unidos mediante una recta:

Ahora ya estás preparado para “graficar” un poco. Como siempre, vamos a utilizar el programa wiris. Si pinchas en el enlace, abrirás una página donde hay un ejercicio resuelto, si quieres ver la gráfica de la función correspondiente sólo tienes que pinchar en el igual. Cuando quieras sustituir una incógnita en verde, pincha sobre ella y una vez que así sitúes el cursor del ordenador, escribe tu respuesta (verás que desaparecerá la casilla en verde). Venga, ¡puedes hacerlo!
Pincha aquí para ir a los ejercicios
Recuerda que una función era una relación en la cual a cada x le correspondía una única y. A través de la gráfica de una relación, podemos decidir fácilmente si dicha relación es una función o no. Veamos el siguiente ejemplo:
Después de bañarse en su casa, Ana dibuja un esbozo de gráfica que muestra lo que ocurre con el volumen de agua de su baño en función del tiempo transcurrido.
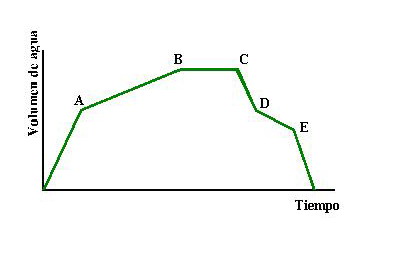

Fíjate que a cada valor del tiempo (eje de las x) le corresponde un único valor del volumen de agua (eje de las y). Pero tengamos presente que un mismo valor de la variable y puede corresponder a diferentes valores de la variable x. Así en el ejemplo, los puntos B y C tienen la misma coordenada y para distintos valores de la x (distintos tiempos). Por decirlo de alguna forma la variable x es “fiel” pero eso no quiere decir que la variable y lo sea, puede serlo o no y la relación de dependencia seguirá siendo una función. Sin embargo, en el momento en que la variable x sea “infiel”, es decir, en el momento en que para una misma x tengamos dos valores de y diferentes la relación de dependencia dejará de ser una función. Como ejemplo de gráfica que no representa una función pincha sobre el siguiente enlace:
Otro ejemplo de gráfica de una relación que no es función sería la siguiente:

Fíjate en que para un mismo valor de la x tenemos hasta 3 valores diferentes de la y. Para verlo mejor, trazamos una recta perpendicular al eje X y vemos que corta a la gráfica en tres puntos diferentes:
