Parábolas
Las funciones denominadas parábolas tienen una ecuación de la forma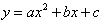 
, donde 
son números cualesquiera (pero 
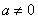ya que si fuera cero lo que tendríamos sería una función lineal, es decir, una recta). Las parábolas suelen tener el siguiente aspecto:
Es decir, una parábola es una función simétrica respecto a un eje de simetría que pasa por su vértice, que por decirlo de alguna forma, es el punto donde la parábola "rebota y da la vuelta". Este vértice tiene siempre por abscisa 
y, como observas, será donde esté localizado el máximo o el mínimo de la función.
Veamos cómo al variar los valores de los coeficientes se va alterando la gráfica de la función. Para ver el efecto de la modificación de cada uno de los coeficientes, vamos a ir estudiando casos sencillos para poder llegar fácilmente a conclusiones.
Caso b = 0 y c = 0
En este caso tenemos que la ecuación de la parábola es 
. La siguiente animación te muestra cómo la variación del coeficiente
hace que la gráfica de la función se modifique:
Observa que al ser b=0 el vértice de la parábola está situado en el punto (0,0) y, por tanto, el eje de simetría de estas parábolas es el eje Y. A medida que la aumenta, la función se hace más "estilizada", más estrecha, porque la función cuanto mayor sea la , más rápidamente crecerá (como puedes observar en la animación, a mayor el punto de la función con abscisa x=1 cada vez está más arriba). Además, si la se hace negativa, la parábola queda abierta hacia abajo, no hacia arriba como es el caso para la positiva.
Caso b = 0
Ahora tendremos que la ecuación de la parábola será de la forma 
. Ya hemos visto el efecto de modificar . Vamos a ver ahora, en la siguiente animación, los efectos de variar c con a=1 fija :
Vemos que al variar el coeficiente c lo que hacemos es que la altura a la que está situado el vértice de la parábola sube o baja según c aumenta o disminuye respectivamente. Al ser b=0, el vértice de la parábola para este caso está situado en (0,c), con lo que al hacerse c negativo tendremos que el vértice de la parábola estará por debajo del eje X.
Caso c = 0
Para este caso tendremos que la ecuación de la parábola será 
. Vamos a ver los efectos de variar b con a=1 fija:
Como observas, el vértice de la parábola se desplaza tanto a lo largo del eje Y como del eje X. Esto es porque, como c=0, el vértice de la parábola se sitúa en 
, así que al variar b con a fija, modificas tanto la abscisa como la ordenada del vértice.
Caso general
Si ahora pinchas aquí podrás ver la gráfica de la parábola más general , pudiendo además variar los coeficientes a la vez.